Technical Papers

Q&A for Deep Combiner for Independent and Correlated Pixel Estimates

Abstract: Monte Carlo integration is an efficient method to solve a high-dimensional integral in light transport simulation, but it typically produces noisy images due to its stochastic nature. Many existing methods, such as image denoising and gradient-domain reconstruction, aim to mitigate this noise by introducing some form of correlation among pixels. While those existing methods reduce noise, they are known to still suffer from method-specific residual noise or systematic errors. We propose a unified framework that reduces such remaining errors. Our framework takes a pair of images, one with independent estimates, and the other with the corresponding correlated estimates. Correlated pixel estimates are generated by various existing methods such as denoising and gradient-domain rendering. Our framework then combines the two images via a novel combination kernel. We model our combination kernel as a weighting function with a deep neural network that exploits the correlation among pixel estimates. To improve the robustness of our framework for outliers, we additionally propose an extension to handle multiple image buffers. The results demonstrate that our unified framework can successfully reduce the error of existing methods while treating them as black-boxes.

Author(s)/Presenter(s):
Jonghee Back, Gwangju Institute of Science and Technology, South Korea
Binh-Son Hua, VinAI Research, VinUniversity, Vietnam
Toshiya Hachisuka, University of Tokyo, Japan
Bochang Moon, Gwangju Institute of Science and Technology, South Korea

---

Q&A for Neural Control Variates

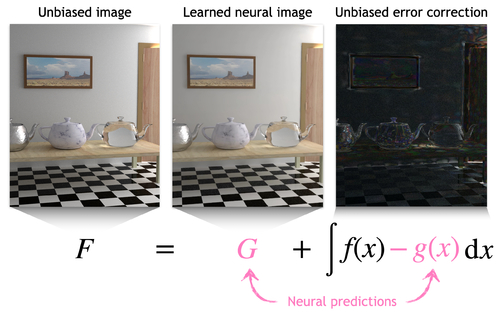
Abstract: We propose neural control variates (NCV) for unbiased variance reduction in parametric Monte Carlo integration. So far, the core challenge of applying the method of control variates has been finding a good approximation of the integrand that is cheap to integrate. We show that a set of neural networks can face that challenge: a normalizing flow that approximates the shape of the integrand and another neural network that infers the solution of the integral equation. We also propose to leverage a neural importance sampler to estimate the difference between the original integrand and the learned control variate. To optimize the resulting parametric estimator, we derive a theoretically optimal, variance-minimizing loss function, and propose an alternative, composite loss for stable online training in practice. When applied to light transport simulation, neural control variates are capable of matching the state-of-the-art performance of other unbiased approaches, while providing means to develop more performant, practical solutions. Specifically, we show that the learned light-field approximation is of sufficient quality for high-order bounces, allowing us to omit the error correction and thereby dramatically reduce the noise at the cost of negligible visible bias.

Author(s)/Presenter(s):
Thomas Müller, NVIDIA, Germany
Fabrice Rousselle, NVIDIA, Switzerland
Alexander Keller, NVIDIA, Germany
Jan Novák, NVIDIA, Switzerland

---

Q&A for Screen-Space Blue-Noise Diffusion of Monte Carlo Sampling Error via Hierarchical Ordering of Pixels

Abstract: We present a novel technique for diffusing Monte Carlo sampling error as a blue noise in screen space. We show that automatic diffusion of sampling error can be achieved by ordering the pixels in a way that preserves locality, such as Z-ordering, and assigning the samples to them from successive sub-sequences of a single low-discrepancy sequence, thus securing well-distributed samples for each pixel, local neighborhoods, and the hole image. We further show that a blue-noise distribution of the error is attainable by scrambling the Z-ordering to induce isotropy. We present an efficient technique to implement this hierarchical scrambling by defining a context-free grammar that describes infinite self-similar lookup trees. Our concept is scalable to arbitrary image resolutions, sample dimensions, and sample count, and supports progressive and adaptive sampling.

Author(s)/Presenter(s):
Abdalla G. M. Ahmed, King Abdullah University of Science and Technology (KAUST), Saudi Arabia
Peter Wonka, King Abdullah University of Science and Technology (KAUST), Saudi Arabia

---

Q&A for Unbiased Warped-Area Sampling for Differentiable Rendering

Abstract: Differentiable rendering computes derivatives of the light transport equation with respect to arbitrary 3D scene parameters, and enables various applications in inverse rendering and machine learning. We present an unbiased and efficient differentiable rendering algorithm that does not require explicit boundary sampling. We apply the divergence theorem to the derivative of the rendering integral to convert the boundary integral into an area integral. We rewrite the converted area integral to a form that is suitable for Monte Carlo rendering. We then develop an efficient Monte Carlo sampling algorithm for solving the area integral. Our method can be easily plugged into a traditional path tracer and does not require dedicated data structures for sampling boundaries.

Author(s)/Presenter(s):
Sai Praveen Bangaru, Massachusetts Institute of Technology, United States of America
Tzu-Mao Li, Massachusetts Institute of Technology, United States of America
Fredo P. Durand, Massachusetts Institute of Technology, United States of America

---

Q&A for Path Differential-Informed Stratified MCMC and Adaptive Forward Path Sampling

Abstract: Markov Chain Monte Carlo (MCMC) rendering is extensively studied, yet it remains largely unused in practice. We propose solutions to several practicability issues, opening up path space MCMC to become an adaptive sampling framework around established Monte Carlo (MC) techniques. We address non-uniform image quality by deriving an analytic target function for image-space sample stratification. The function is based on a novel connection between variance and path differentials, allowing analytic variance estimates for MC samples, with potential uses in other adaptive algorithms outside MCMC. We simplify these estimates down to simple expressions using only quantities known in any MC renderer. We also address the issue that most existing MCMC renderers rely on bi-directional path tracing and reciprocal transport, which can be too costly and/or too complex in practice. Instead, we apply our theoretical framework to optimize an adaptive MCMC algorithm that only uses forward path construction. Notably, we construct our algorithm by adapting (with minimal changes) a full-featured path tracer into a single-path state space Markov Chain, bridging another gap between MCMC and existing MC techniques.

Author(s)/Presenter(s):
Tobias Zirr, Karlsruhe Institute of Technology (KIT), Germany
Carsten Dachsbacher, Karlsruhe Institute of Technology (KIT), Germany

---

Back