Technical Papers

Q&A for Bijective Projection in a Shell

Abstract: We introduce an algorithm to convert a self-intersection free, orientable, and manifold triangle mesh into a generalized prismatic shell equipped with a bijective projection operator to map the triangle mesh to a class of discrete surfaces contained within the shell whose normals satisfy a simple local condition. Properties can be robustly and efficiently transferred between these surfaces using the prismatic layer as a common parametrization domain. The combination of the prismatic shell construction and corresponding projection operator is a robust building block readily usable in many downstream applications, including the solution of PDEs on surfaces, displacement maps synthesis, Boolean operations, tetrahedral meshing, geometric textures, collision proxies, and animation cages.

Author(s)/Presenter(s):
Zhongshi Jiang, New York University, United States of America
Teseo Schneider, New York University, United States of America
Denis Zorin, New York University, United States of America
Daniele Panozzo, New York University, United States of America

---

Q&A for Conforming Weighted Delaunay Triangulations

Abstract: Given a set of points together with a set of simplices we show how to compute weights associated with the points such that the weighted Delaunay triangulation of the point set contains the simplices, if possible. For a given triangulated surface, this process provides a tetrahedral mesh conforming to the triangulation, i.e. solves the problem of meshing the triangulated surface without inserting additional vertices. The restriction to weighted Delaunay triangulations ensures that the orthogonal dual mesh is embedded, facilitating common geometry processing tasks. We show that the existence of a single simplex in a weighted Delaunay triangulation for given vertices amounts to a set of linear inequalities, one for each vertex. This means that the number of inequalities for a given triangle mesh is quadratic in the number of mesh elements, making the naive approach impractical. We devise an algorithm that incrementally selects a small subset of inequalities, repeatedly updating the weights, until the weighted Delaunay triangulation contains all constrained simplices or the problem becomes infeasible. Applying this algorithm to a range of triangle meshes commonly used graphics demonstrates that many of them admit a conforming weighted Delaunay triangulation, in contrast to conforming or constrained Delaunay that require additional vertices to split the input primitives.

Author(s)/Presenter(s):
Marc Alexa, TU Berlin, Germany

---

Q&A for You Can Find Geodesic Paths in Triangle Meshes by Just Flipping Edges

Abstract: This paper describes a new approach to computing exact geodesics on polyhedral surfaces. The basic idea is to perform edge flips, in the same spirit as the classic Delaunay flip algorithm. As a natural byproduct of this process, one also obtains a triangulation containing the shortened paths as edges. More precisely, given a path as a sequence of mesh edges, we transform it into a locally shortest geodesic path while avoiding self-crossings (i.e., we find a geodesic in the same isotopy class). Implementation amounts to a simple subroutine that flips edges to create a shorter path within their local neighborhood. The method is guaranteed to produce an exact geodesic path in a finite number of operations; practical runtimes are on the order of a few milliseconds, even for meshes with millions of faces. It is easily applied to cases beyond simple paths, including closed loops, curve networks, and multiply-covered curves. The method is well-suited for applications in geometry processing: it guarantees that curves do not cross, a necessary property when straightening region boundaries or cut networks, and furthermore it yields an intrinsic triangulation which includes the geodesic curves as edges, extending the idea of a \emph{constrained Delaunay triangulation} to curved surfaces. Evaluation on large datasets indicates that the method is both efficient and robust even for challenging models with low-quality triangulations. We explore how the curves and triangulations produced by the method facilitate a variety of tasks in digital geometry processing such as straightening cuts and segmentation boundaries, computing geodesic Bézier curves, and providing accurate boundary conditions for PDEs.

Author(s)/Presenter(s):
Nicholas Sharp, Carnegie Mellon University, United States of America
Keenan Crane, Carnegie Mellon University, United States of America

---

Q&A for Fast and Robust Mesh Arrangements using Floating-point Arithmetic

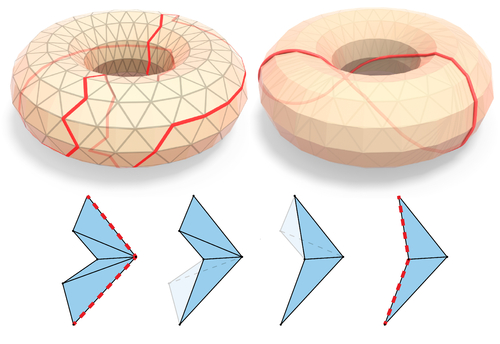
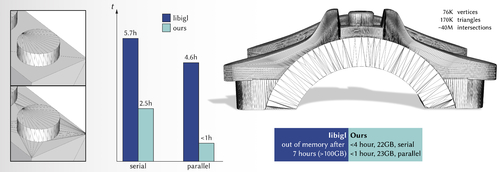
Abstract: We introduce a novel algorithm to transform any generic set of triangles in 3D space into a well-formed simplicial complex. Intersecting elements in the input are correctly identified, subdivided, and connected to arrange a valid configuration, leading to a topologically sound partition of the space into piece-wise linear cells. Our approach does not require the exact coordinates of intersection points to calculate the resulting complex. We represent any intersection point as an unevaluated combination of input vertices. We then extend the recently introduced concept of indirect predicates [Attene2020] to define all the necessary geometric tests that, by construction, are both exact and efficient since they fully exploit the floating-point hardware. This design makes our method robust and guaranteed correct, while being virtually as fast as non-robust floating-point based implementations. Compared with existing robust methods, our algorithm offers a number of advantages: it is much faster, has a better memory layout, scales well on extremely challenging models, and allows fully exploiting modern multi-core hardware with a parallel implementation. We thoroughly tested our method on thousands of meshes, concluding that it consistently outperforms prior art. We also demonstrate its usefulness in various applications, such as computing efficient mesh booleans, Minkowski sums, and volume meshes.

Author(s)/Presenter(s):
Gianmarco Cherchi, University of Cagliari, Italy
Marco Livesu, CNR-IMATI: GENOVA, Italy
Riccardo Scateni, University of Cagliari, Italy
Marco Attene, CNR-IMATI: GENOVA, Italy

---

Q&A for Fast Construction of Discrete Geodesic Graphs

Abstract: This paper develops a new method for constructing Discrete Geodesic Graph (DGG)—an undirected, sparse graph for computing discrete geodesic distances and paths on triangle meshes. Based on a novel accuracy aware window propagation scheme, our method is able to compute the graph edges in a direct and efficient manner. Given a triangle mesh with n vertices and a user-specified accuracy parameter ɛ, our method produces a DGG with O(n\√ɛ) edges in empirical O(n\ɛ0.75 log 1\ɛ) time, which greatly improves the time complexity O(n\ɛ log 1\ɛ) of the existing method. Extensive evaluation on a large-scale 3D shape repository shows that our method is efficient and can produce high-quality geodesic distances with predictable accuracy and guaranteed true distance metric. In particular, our method has a great advantage over the existing approximate methods on meshes with high degree of anisotropy. The source code is available at https://github.com/GeodesicGraph..

Author(s)/Presenter(s):
Yohanes Yudhi Adikusuma, Nanyang Technological University, Singapore
Zheng Fang, Nanyang Technological University, Singapore
Ying He, Nanyang Technological University, Singapore

---

Back