Technical Papers

Q&A for Opening and Closing Surfaces

Abstract: We propose a new type of curvature flow for curves in 2D and surfaces in 3D. The flow is inspired by the mathematical morphology opening and closing operations. These operations are classically defined by composition of dilation and erosion operations. In practice, existing methods implemented this way will result in re-discretizing the entire shape, even if some parts of the surface do not change. Instead, our surface-only curvature-based flow moves the surface selectively in areas that should be repositioned. In our triangle mesh discretization, vertices in regions unaffected by the opening or closing will remain exactly in place.

Author(s)/Presenter(s):
Silvia Sellán, University of Toronto, Canada
Jacob Kesten, Rice University, United States of America
Yan Sheng Ang, National University of Singapore, Singapore
Alec Jacobson, University of Toronto, Canada

---

Q&A for Nonlinear Spectral Geometry Processing via the TV Transform

Abstract: We introduce a novel computational framework for digital geometry processing, based upon the derivation of a nonlinear operator associated to the total variation functional. Such operator admits a generalized notion of spectral decomposition, yielding a sparse multiscale representation akin to Laplacian-based methods, while at the same time avoiding undesirable over-smoothing effects typical of such techniques. Our approach entails accurate, detail-preserving decomposition and manipulation of 3D shape geometry while taking an especially intuitive form: non-local semantic details are well separated into different bands, which can then be filtered and re-synthesized with a straightforward linear step. Our computational framework is flexible, can be applied to a variety of signals, and is easily adapted to different geometry representations, including triangle meshes and point clouds. We showcase our method throughout multiple applications in graphics, ranging from surface and signal denoising to detail transfer and cubic stylization.

Author(s)/Presenter(s):
Marco Fumero, Sapienza University of Rome, Italy
Michael Moeller, University of Siegen, Germany
Emanuele Rodolà, Sapienza University of Rome, Italy

---

Q&A for Shape Approximation by Developable Wrapping

Abstract: We present an automatic tool to approximate curved geometries with piecewise developable surfaces. At the center of our work is an algorithm that wraps a given 3D input surface with multiple developable patches, each modeled as a discrete orthogonal geodesic net. Our algorithm features a global optimization routine for effectively finding the placement of the developable patches. After wrapping the mesh, we use these patches and a non-linear projection step to generate a surface that approximates the original input, but is also amendable to simple and efficient fabrication techniques thanks to being piecewise developable. Our algorithm allows users to steer the tradeoff between approximation power and the number of developable patches used. We demonstrate the effectiveness of our approach on a range of 3D shapes. Compared to previous approaches, our results exhibit a smaller or comparable error with fewer patches to fabricate.

Author(s)/Presenter(s):
Alexandra Ion, ETH Zürich, Switzerland
Michael Rabinovich, ETH Zürich, Switzerland
Philipp Herholz, ETH Zürich, Switzerland
Olga Sorkine-Hornung, ETH Zürich, Switzerland

---

Q&A for To cut or to fill: a global optimization approach to topological simplification

Abstract: We present a novel algorithm for simplifying the topology of a 3D shape, which is characterized by the number of connected components, handles, and cavities. Existing methods either limit their modifications to be only cutting or only filling, or take a heuristic approach to decide where to cut or fill. We consider the problem of finding a globally optimal set of cuts and fills that achieve the simplest topology while minimizing geometric changes. We show that the problem can be formulated as graph labelling, and we solve it by a transformation to the Node-Weighted Steiner Tree problem. When tested on examples with varying levels of topological complexity, the algorithm shows notable improvement over existing simplification methods in both topological simplicity and geometric distortions.

Author(s)/Presenter(s):
Dan Zeng, Washington University in St. Louis, United States of America
Erin Chambers, St. Louis University, United States of America
David Letscher, St. Louis University, United States of America
Tao Ju, Washington University in St. Louis, United States of America

---

Q&A for Sparse Cholesky Updates for Interactive Mesh Parameterization

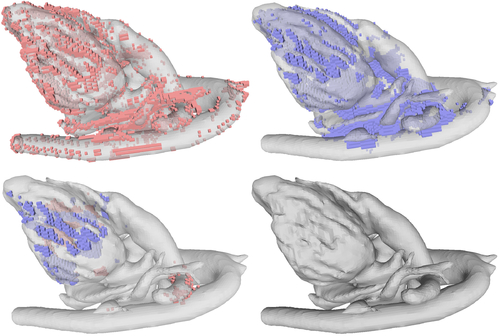
Abstract: We present a novel linear solver for interactive parameterization tasks. Our method is based on the observation that quasi-conformal parameterizations of a triangle mesh are largely determined by boundary conditions. These boundary conditions are typically constructed interactively by a user who has to take several artistic and geometric constraints into account while introducing cuts on the geometry. Commonly, the main computational burden in these methods is solving a linear system every time new boundary conditions are imposed. The core of our solver is a novel approach to efficiently update the Cholesky factorization of the linear system to reflect new boundary conditions, thereby enabling a seamless and interactive workflow even for larger meshes consisting of several millions of vertices.

Author(s)/Presenter(s):
Philipp Herholz, ETH Zürich, Switzerland
Olga Sorkine-Hornung, ETH Zürich, Switzerland

---

Q&A for Constructing 3D Self-Supporting Surfaces with Isotropic Stress Using 4D Minimal Hypersurfaces of Revolution

Abstract: We formulate the over-constrained 3D equilibrium problem into a volume minimization problem in 4D and figure out a sufficient condition of 3D self-supporting structures with isotropic stresses.

Author(s)/Presenter(s):
Long Ma, Shandong University, Nanyang Technological University, China
Ying He, Nanyang Technological University, Singapore
Qian Sun, Tianjin University, China
Yuanfeng Zhou, Shandong University, China
Caiming Zhang, Shandong University, China
Wenping Wang, University of Hong Kong, Hong Kong

---

Back